La découverte de dalles étranges sur mon terrain
Il y avait sur mon terrain une pile de dalles en béton de formes irrégulières. Pensant qu’elles étaient conçues pour s’assembler, j’en ai disposé quelques-unes sur le sol à la façon d’un pavage :
Curieusement, ces dalles, toutes identiques, en forme d’hexagone, forment un pavage qui semble irrégulier.
Comment caractériser cette forme géométrique ?
J’ai voulu connaître les caractéristiques géométriques de ces hexagones, j’ai remarqué tout de suite que la forme est symétrique et que les côtés adjacents sont égaux deux par deux, quatre formant un angle de 120° et deux un angle de 90°. J’ai ensuite relevé les longueurs des côtés et des diagonales de façon à pouvoir tracer le polygone à l’échelle au moyen d’un logiciel de dessin (Libre Office Draw).
Puis j’ai recherché des formes équivalentes sur internet, et je suis tombé sur un article (en anglais) de Michael de Villiers expliquant la construction de l’hexagone de Haag, dont la particularité est de pouvoir former un assemblage plan sans vide, autrement dit un pavage, on dira donc que la caractéristique de l’hexagone de Haag est d’être pavable :
1ère méthode de construction :
Soit ABC un triangle équilatéral et F un point quelconque.
Choisir le point D pour que AF = AD et ∠DAF = 120 °.
Choisir le point E pour que BE = BD et ∠DBE = 120 °.
Il s’ensuit que CE = CF et ∠ECF = 120 °.
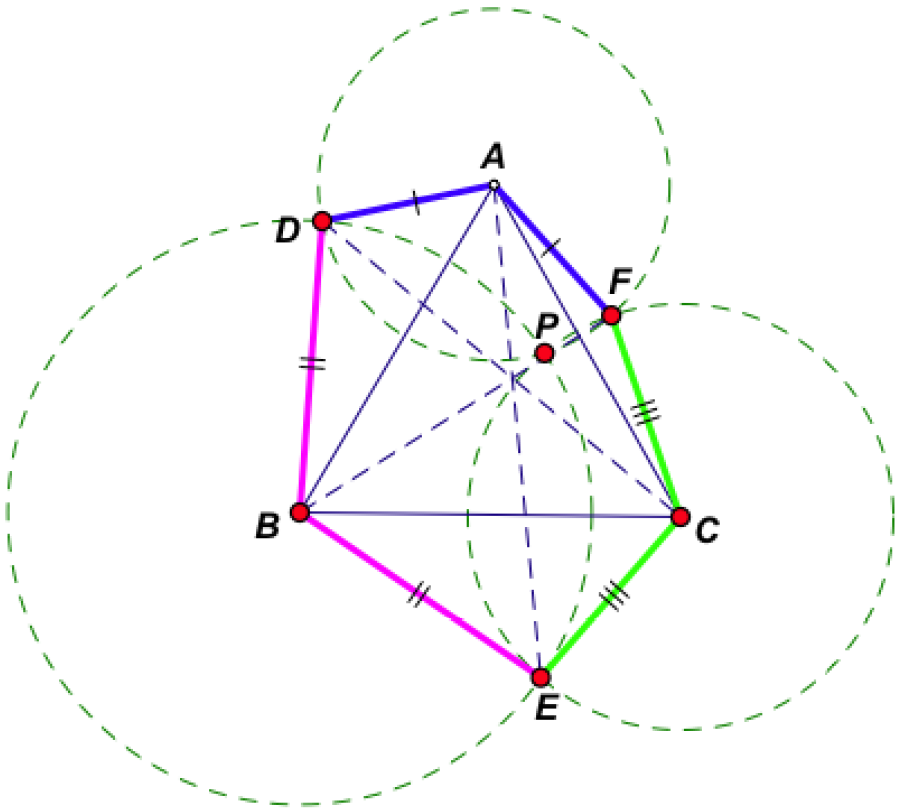
2ème méthode de construction :
Construire un triangle équilatéral △ ABC.
Dessiner un cercle de centre A et de rayon arbitraire AD.
Construire un cercle de centre B et de rayon BD.
Désigner par P l’autre intersection des deux cercles centrés en A et B.
Tracer un cercle de centre C et de rayon CP.
Désigner respectivement par E et F les autres intersections du cercle C avec les cercles B et C.
Il s’ensuit que ∠DAF = ∠DBE = ∠ECF = 120 ° et que ADBECF est un hexagone pavable de Haag.
Revenons à mes dalles
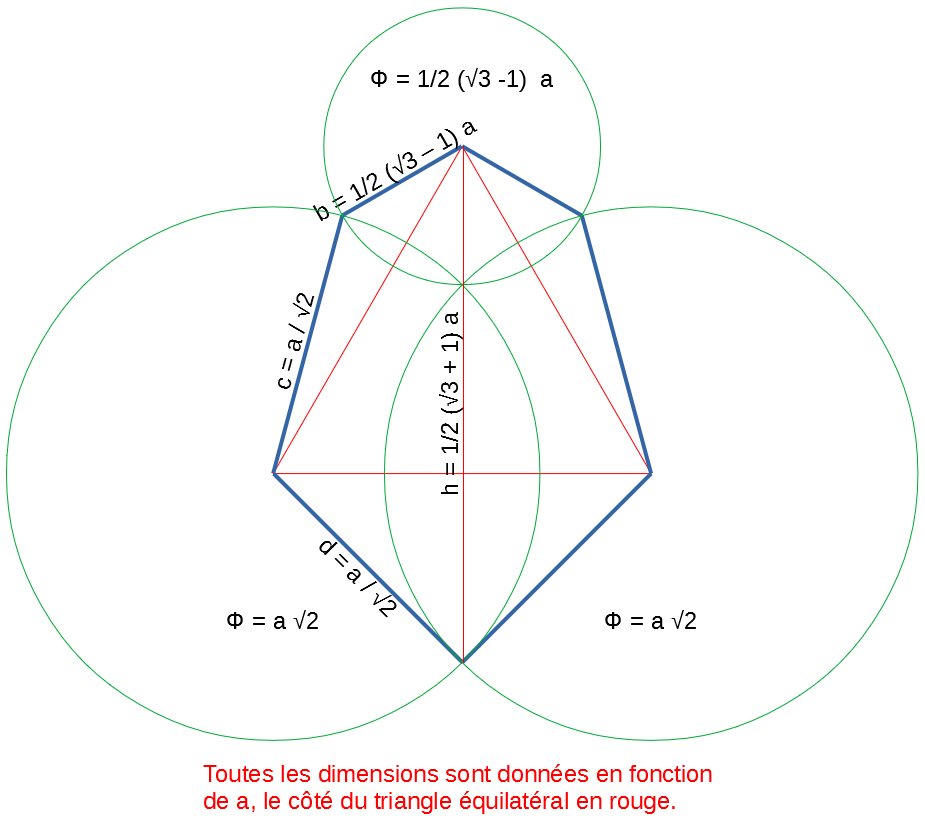
J’ai adapté ce dessin au cas particulier des dalles de mon jardin et j’ai construit l’hexagone de Haag. Comme il s’agit d’un cas particulier : forme symétrique, un angle droit, j’ai pu calculer les différentes longueurs et les exprimer en fonction de la longueur du côté du triangle équilatéral inscrit :
Il ne me restait plus qu’à démontrer que mon hexagone était pavable :
J’ignore si de tels pavés sont actuellement disponibles dans le commerce, mais ils sont relativement faciles à réaliser avec un moule formé d’un fond sur lequel reposent 6 tasseaux en bois assemblés.
Existe-t-il d’autres hexagones pavables ?
Oui, l’hexagone de Haas n’est pas le seul hexagone pavable, il en existe trois, l’hexagone de Haas étant le numéro 3 (Wikipedia EN) :
L’hexagone régulier, quant à lui, répond aux critères des trois catégories.
Quels sont les polygones pavables ?
Nous avons vu que’il n’existe que 3 types d’hexagones pavables, voyons maintenant les autres polygones :
Seuls le triangle, le quadrilatère, le pentagone et l’hexagone sont pavables.
Tous les triangles et tous les quadrilatères sont pavables, y compris bien sûr le triangle équilatéral et le carré.
Tous les pentagones ne sont pas pavables, seuls 15 types (Wikipedia EN) de pentagones sont pavables. Le pentagone régulier n’est pas pavable dans le plan, mais il l’est dans l’espace, sous la forme du dodécaèdre régulier.
Toutes les informations que j’ai trouvées sur ces polygones particuliers proviennent de sites en langue anglaise, sur un même sujet, les informations de Wikipedia FR sont parcellaires et incomplètes en comparaison avec Wikipedia EN.